Multiplicity in Clinical Trials

Introduction

• Type I error rate inflated when conducting multiple hypothesis tests $(m)$ each with the nominal 0.05 significance level $(\alpha)$ --> the multiplicity problem
• Source of multiplicity in clinical trials
  • multiple arms
  • control for more than one endpoint
  • control for more than one population
  • control repeatedly in time
  • etc.
• Dealing with multiplicity
  • Reducing the degree of multiplicity
    • limit the number of questions
    • minimize the number of variables by using e.g. composite endpoints, summary statistic, etc.
    • Prioritizing questions
  • If multiplicity still persists
    • multiplicity adjustment (refer to regulatory guidance)

Common multiple test procedures

Basic concepts

• Family-wise error rate (FWER): overall type I error rate when testing a family of null hypotheses

  • aim: $Pr(\text{reject at least one true null}) \le \alpha$

• Ajusted p-values: extend ordinary (i.e. unadjusted) p-values by adjusting them for a given multiple test procedure, which can be compared directly with the significance level 𝛼, while controlling the FWER

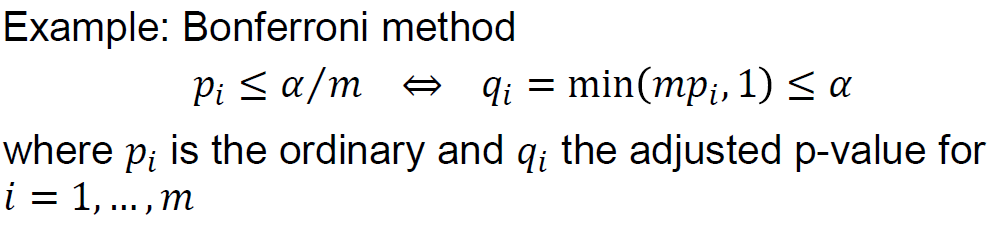
  • Formally, the adjusted p-value is the smallest significance level at which a given hypothesis is significant as part of the multiple test procedure. e.g.

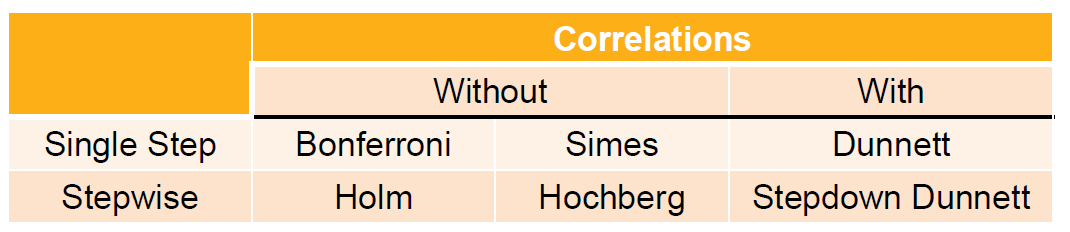
• Single step methods

  • The rejection or non-rejection of a single hypothesis does not depend on the decision on any other hypothesis.
  • e.g. Bonferroni, Simes, Dunnett, etc.

• Stepwise methods

  • The rejection or non-rejection of a particular hypothesis may depend on the decision on other hypotheses.
  • e.g. Holm, Hochberg, stepdown Dunnett, …

Methods

Bonferroni

• Use 𝛼/𝑚 for all inferences; for 𝑖=1,…,𝑚: $$\text{Reject } H_i \text{ if } p_i \le \alpha/m$$ or with adjusted p-values $q_i = \min(mp_i, 1)$, $$\text{Reject } H_i \text{ if } q_i \le \alpha$$
• This method follows the idea of Boole's inequality: $Pr(\cup A_i)\le \sum_i Pr(A_i)$, where $A_i = \{p_i\le \alpha/m\}$ denotes the event of rejecting $H_i$
• Properties
  • Conservative if the number of hypotheses is large or the test statistics are strongly positively correlated
  • Can be improved by using stepwise methods (e.g. Holm procedure) and accounting for correlations (e.g. Dunnett test)
  • Rarely used in practice but is the basis for commonly used advanced procedures

Holm

• Overview
  • Using ordinary p-values
  • Using ajusted p-values
• Properties
  • A stepwise procedure and more powerful than Bonferroni method
  • Sometimes called "stepdown Bonferroni" procedure
  • Can be improved by accounting for correlations (e.g. stepdown Dunnett test)

Simes

• Overview

• Comparison with Bonferroni

  • Simes is more powerful than a global test based on Bonferroni
  • Simes assumes non-negative correlations between p-values, Bonferroni doesn't

Hochberg (stepwise version of Simes method/stepup Simes)

• Overview
• Properties
  • Stepup Simes
  • More powerful than Holm procedure
    • Both use same thresholds, but Hochberg starts with the largest p-value, whereas Holm starts with the smallest
  • It makes same assumption as the Simes test, i.e. independence or positive dependence of p-values
  • Can be improved, e.g. Hommel procedure based on the closed test procedure.

Dunnett

• When comparing several treatments with a control

• Other methods mentioned above can also be used but only Dunnett test exploits the correlation between the p-values

• Overview

  • linear model and hypotheses
  • individual test statistics
  • rejection rule

• Properties

  • Single step test, which is better than Bonferroni as it exploits the known correlations between test statistics
  • Adjusted p-values can be calculated numerically based on the multivariate t-distribution
  • The Dunnett test shown here can be extended to any linear and generalized linear model
  • It can be improved by extending it to a stepwise procedure, similar to the Holm procedure
  • Other well-known parametric tests follow the same principle. For example, the Tukey test compares all treatment groups against each other, also using a multivariate 􀝐-distribution

Stepwise Dunnett

• Overview

• Properties

  • the quantiles change as hypotheses are rejected; e.g. if $H_{(1)}$ is rejected, then the quantile $c_{m-1, 1-\alpha}$ is computed from a (m-1)-variate t-distribution
  • the stepwise Dunnett test is better than the single step Dunnett test
    • it can be shown that $c_{m, 1-\alpha} \ge c_{m-1, 1-\alpha}\le \cdots \le c_{1, 1-\alpha}$, where $c_{1, 1-\alpha} = t_{v, 1-\alpha}$ is the quantile from the univariate t-distribution with $v$ degrees of freedom
    • The Dunnett test uses $c_{m, 1-\alpha}$ for all comparisons
  • the stepwise Dunnet test is better than the Holm procedure as it exploits the known correlations between test statistics
    • The stepwise version shown here is sometimes called "stepdown Dunnett" test
    • A "stepup Dunnett" test also exist, similar to Hochberg

Summary

• Stepwise methods are preferred over single step methods, which are less powerful and less used in practice
• Accounting for correlations leads to more powerful procedures, but correlations are not always known
• Simes-based methods are more powerful than Bonferroni-based methods, but control the FWER only under certain dependence structure
• In practice, we select the procedure that is not only powerful from a statistical perspective, but also appropriate from clinical perspective

Hierarchical test procedure

Background

• Previous multiple tests methods do not reflect the relative importance of the two endpoints, which is usually the case in RCT, where we have primary/secondary/exploratory endpoints with ordered importance
• Previous stepwise procedures use a data-driven order of hypotheses, whereas in the RCT setting we need a multiple test procedure that specifies the order of the hypothesis based on clinical importance
• Hierarchical test procedure: the hierarchy of hypotheses is specified before data is observed

Fixed sequence procedure

• Overview

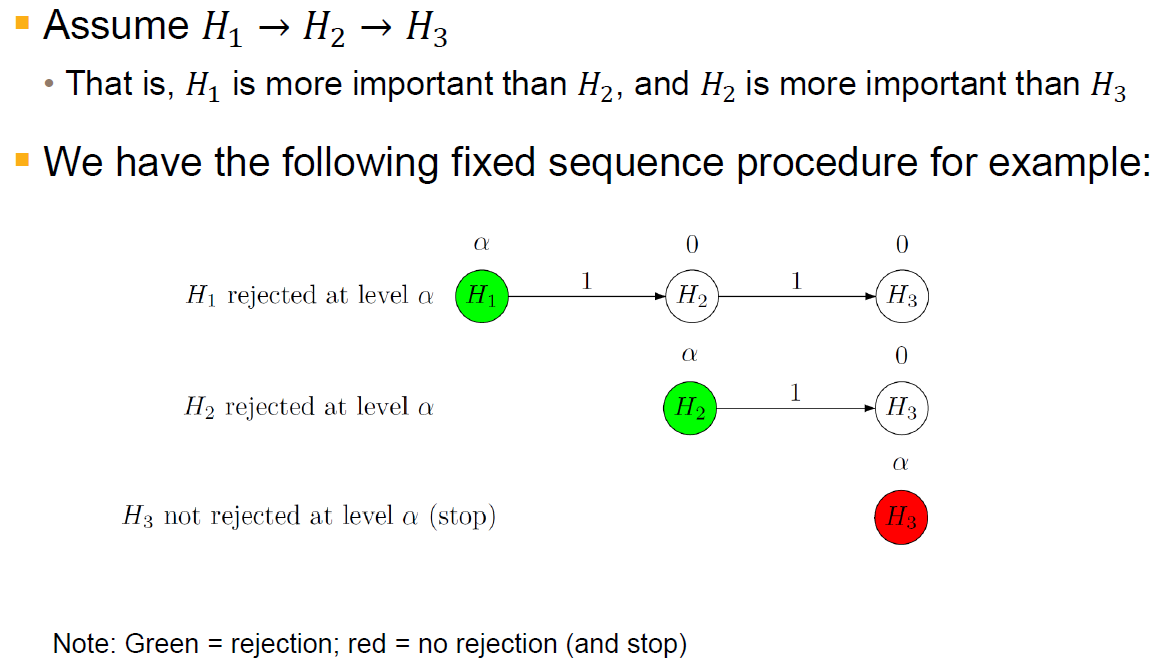
• Properties

  • Adjusted p-values are given by $q_i = \max\{p_1, \cdots, p_i\}, i = 1, \cdots, m$
  • Advantages
    • Simple
    • Optimal when hypotheses early in the sequence are associated with large effects and performs poorly otherwise
  • Disadvantages
    • Once a hypothesis is not rejected, no further testing is permitted
  • Great care is advised when specifying the sequence of hypotheses

Fallback procedure

• Overview

• Properties

  • The fixed sequence procedure is obtained as a special case from the fallback procedure by setting $\alpha_1=\alpha$ and $\alpha_i=0$ for $i>1$
  • In contrast to the fixed sequence procedure, fallback procedure tests all hypotheses in the pre-specified sequence even if the intitial hypotheses are not rejected

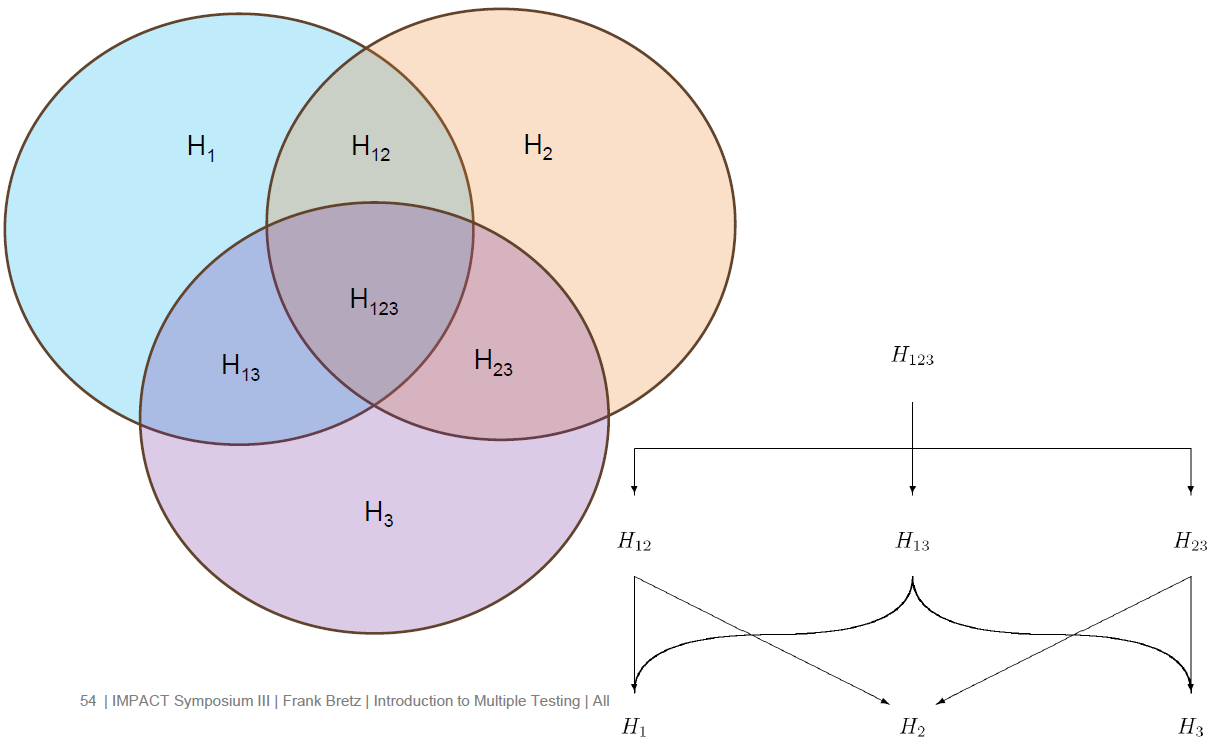
Closed test procedure (CTP)

• Overview/formal definition
  • Test the iteraction hypotheses using Bonferroni, Simes, Dunnett, etc. at level $\alpha$
  • Test each individual hypothesis at level $\alpha$

CTP using Bonferroni ( == Holm procedure)

CTP usign Simes

• When m=2, it's equivalent to Hochberg procedure
• When m>2, it's less powerful

CTP using Dunnett

• This is equivalent to stepdown Dunnett procedure

CTP using weighted Bonferroni

• The first is equivalent to the the fixed sequence procedure

• The second version is equivalent to the fallback procedure

What if more than two hypotheses?

• Do CTP for pairwise combinations

Summary

Summary and Conclusions

• Closed test procedure is a general principle to construct powerful multiple test procedures; many common procedures are CTPs
• For structured hypotheses, one can apply the graphical approach, which is based on CTPs
• It is critical to choose the suitable method for a particular problem
• There are different types of multiplicity problems that need other methods than those described here, such as:
  • Safety data analyses
  • Large-scale testing in genetics, proteomics etc.
  • Post-hoc analyses / data snooping

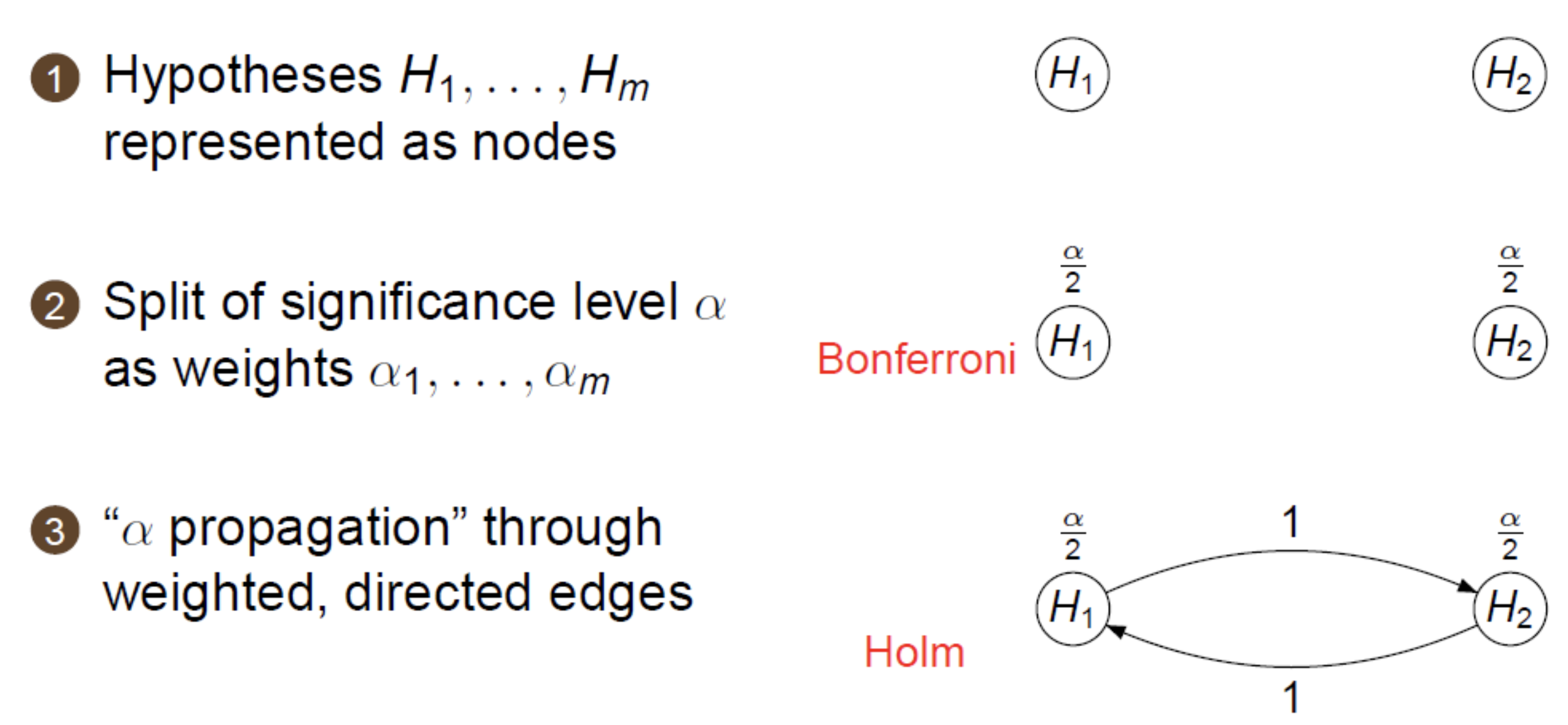
Graphical approach^[1][2]

• Initial allocation of the significance level to $m$ hypothesis: $\alpha_1 + \cdots + \alpha_m = \alpha$
• $\alpha$-propagation: if a hypothesis $H_i$ is rejected at level $\alpha_i$, propagate its level $\alpha_i$ to the remaining, not yet rejected hypotheses (according to aprefixed rule) and continue testing with the updated $\alpha$ levels

Conventions

Weighted Holm procedure: i.e. $\alpha$ is no longer evenly splited among hypotheses

Common multiple test procedues

• Fixed sequence procedure
• Fallback procedure

Formal description

• Initial levels $\alpha = (\alpha_1, \cdots, \alpha_m)$ with $\sum_{i=1}^m\alpha_i = \alpha \in (0, 1)$

• $m \times m$ Transition matrix $\bf{G}=(g_{ij})$, Where $g_{ij}$ is the fraction of the level of $H_i$ that is propagated to $H_j$ with $0\le g_{ij} \le 1, g_{ii} = 0$ and $\sum_{j=1}^mg_{ij}\le1, \forall i=1, \cdots, m$

  ($G, a$) determine a graph with an associated multiple test

• Update algorithm

  

• The initial levels $\alpha$, the transition matrix 𝑮, and the algorithm define a unique sequentially rejective test procedure that controls the FWER at level $\alpha$

• Any multiple test procedure derived and visualized by a graph ($G, \alpha$) is based on the closed test principle

• The graph ($G, \alpha$) and the algorithm define weighted Bonferroni tests for each intersection hypothsis in a CTP

• The algorithm defines a shortcut for the resulting CTP, which does not depend on the rejection sequence

• Tools: R {gMPA} package

Summary

• Tailor advanced multiple test procedures to structured families of hypotheses
• Visualize complex decision strategies in an efficient and easily communicable way
• Ensure strong FWER control
• It covers many common multiple test procedures as specifal cases: Holm, fixed sequence, fallback, gatekeeping, etc.

References